Grundlegende Betrachtungen zur Modellierung transienter thermischer Vorgänge beim selektiven Lasersintern von Thermoplasten
© 2011 Dominik Rietzel; Lizenznehmer RTejournal, weitere Informationen sind zu finden unter: http://www.dipp.nrw.de/service/dppl/
urn:nbn:de:0009-2-29980
Zusammenfassung
Die komplexen transienten thermischen Bauraumverhältnisse während der Schichtgenerierung beim Lasersintern von Thermoplasten haben direkten Einfluss auf die resultierenden Bauteileigenschaften. Dies schlägt sich in Effekten wie dem „Curl“ oder Bauteilverzug nieder. Ohne Kenntnisse über die zeitlichen und örtlichen Temperaturverhältnisse im Bauraum können weder der gesamte Bauraum ausgenutzt, noch die späteren Bauteileigenschaften vorhergesagt werden. Folglich wird die Wirtschaftlichkeit des Verfahrens im Hinblick auf einen Einsatz zur Serienproduktion begrenzt. Neben der experimentellen Erforschung der transienten thermischen Zustände während des Lasersinterns ist die Modellbildung zur simulativen Abbildung ebendieser von großer Bedeutung. Dieser Beitrag stellt den grundlegenden Aufbau eines Simulationsmodells für die schichtweise Bauteilgenerierung dar und zeigt allgemeine Modellierungsansätze für die charakteristischen thermischen Materialkennwerte von Pulvern auf. Weiterhin erfolgt anhand einer Parameterstudie eine Quantifizierung der Effekte einzelner Materialeigenschaften und Prozessstellgrößen auf die mittels finiter Elemente Methode berechneten Temperaturverhältnisse an einer Pulverschicht.
Abstract
The transient thermal conditions, while the layer-wise built-up of thermoplastic parts, in the building chamber have a big influence on processing and resulting part properties. Especially effects like warpage or curl can be seen. Without detailed knowledge about the time and place dependent thermal circumstances it is not possible to use the whole size of the building chamber or to predict later properties of components. Consequently the efficiency of the process is limited particularly with regard to series production. Besides the experimental investigation the theoretical modeling of the transient thermal circumstances during the building process matters. This paper presents the basic build-up of a simulation model for the layer-wise part building process. Furthermore common modeling strategies for characteristic thermal material properties of powders are shown. Moreover the effects of material properties and process parameters on the via finite element method calculated temperature fields are quantified.
Das selektive Lasersintern (SLS) von Thermoplasten ist seit 1992 kommerziell auf dem Technologiemarkt erhältlich und zählt zu den etablierten Verfahren der schichtweisen Bauteilerzeugung [1]. Dabei gewinnt die Serienproduktion von Bauteilen mittels additiver Fertigungsverfahren an Bedeutung, was hohe Anforderungen an die Reproduzierbarkeit der Erzeugnisse stellt [2]. Dazu bedarf es einer detaillierten Kenntnis der werkstofflichen und prozessbestimmenden Fertigungsparameter. Die komplexen transienten thermischen Bauraumverhältnisse während der Schichtgenerierung beim Lasersintern von Thermoplasten haben direkten Einfluss auf die resultierenden Bauteileigenschaften [3]. Dies schlägt sich gerade bei flächigen Bauteilen in Effekten wie dem „Curl“ oder Bauteilverzug nieder. Ohne Kenntnisse über die zeitlichen und örtlichen Temperaturverhältnisse im Bauraum kann dieser weder optimal ausgenutzt, noch die späteren Bauteileigenschaften vorhergesagt werden. Folglich wird die Wirtschaftlichkeit des Verfahrens im Hinblick auf einen Einsatz zur Serienproduktion begrenzt. Zudem steigt der Anteil strukturell komplexer Bauteile, welche gegebenenfalls topologieoptimiert konstruiert wurden. Besonders bei diesen anspruchsvollen Strukturbauteilen mit filigranen Konturen und dünnen Stegen liegen eine Vielzahl an Grenzflächen zwischen Schmelze und umliegendem Pulver vor und die mechanischen Eigenschaften für die Berechnung sind meist nicht experimentell verifiziert. Bei der Fertigung liegen dementsprechend unterschiedlichste zeit- und ortsabhängige Temperaturfelder an, welche experimentell (z.B. für infinitesimal kleine Bereiche) schwer zu erfassen sind.
Neben der experimentellen Erforschung der transienten thermischen Zustände während des Lasersinterns ist die Modellbildung zur simulativen Abbildung ebendieser von großer Bedeutung. Diese Arbeit stellt den grundlegenden Aufbau eines Simulationsmodells für die schichtweise Bauteilgenerierung dar und zeigt erste allgemeine Modellierungsansätze für die charakteristischen thermischen Materialkennwerte von Thermoplastpulvern auf. Weiterhin erfolgt anhand einer Parameterstudie eine Quantifizierung der Effekte einzelner Materialeigenschaften und Prozessstellgrößen auf die mittels finiter Elemente Methode (FEM) berechneten Temperaturverhältnisse an einer Pulverschicht. Die Modellierung der transienten Temperaturfelder während des Bauprozesses, insbesondere von Strukturen, ist eine Grundvoraussetzung zur Beschreibung der bauteilqualitätsbestimmenden Kristallisation im Vorfeld einer Teileproduktion. Diese Arbeit soll die Grundlagen schaffen, um die ablaufenden Prozessvorgänge zukünftig simulieren zu können.
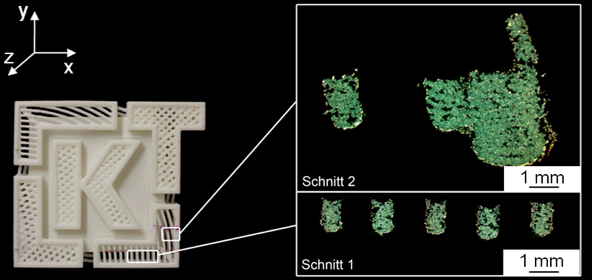
Bild 1: Lasergesinteres Bauteil mit Dünnschnitten zur Darstellung der Wärmeeinflüsse auf Bauteileigenschaften
Grundlage der folgenden Betrachtungen ist das Modell des quasi-isothermen Lasersinterns. Voraussetzung für das Modell des quasi-isothermen Lasersinterns ist die Beobachtung, dass teilkristalline Thermoplasten in einem begrenzten Temperaturbereich dT sowohl als Feststoff als auch Schmelze vorliegen, wie die schematische DSC-Messkurve eines teilkristallinen Thermoplasten in Bild 2 zeigt.
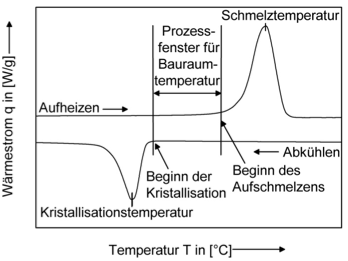
Bild 2: Schematischer DSC-Verlauf eines teilkristallinen Thermoplasten [4]
Innerhalb dieses Zweiphasengebiets liegt die Temperatur des Bauraums nach einer initialen Pulvervorwärmung. Der Laserstrahl bringt während des Bauprozesses an ausgewählten Punkten im Idealfall exakt die Schmelzenthalpie als Aktivierungsenergie für den Flüssigphasensinterprozess in das Pulver ein [5]. Der bestrahlte Bereich schmilzt dabei auf, ohne dass es im umliegenden Pulverbett zu einer Temperaturerhöhung kommt. Die exakte Modellierung thermischer Materialeigenschaften von Pulvern ist zur Beschreibung der transienten thermischen Zustände mittels numerischer Methoden unerlässlich, damit der schmale Temperaturbereich des Zweiphasengebietes teilkristalliner Thermoplaste adäquat im Berechnungsmodell erfasst wird. In Bild 7 sind die thermischen Eigenschaften von Pulvern dargestellt, die als Eingangsgröße in ein Materialmodell einfließen.
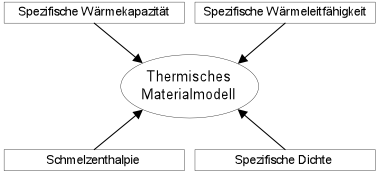
Bild 3: Eingangsgrößen in das thermische Materialmodell
Neben der korrekten Abbildung des Materialverhaltens von teilkristallinen Thermoplastpulvern ist die Modellierung der Laserenergieeinbringung in das Pulverbett von entscheidender Bedeutung für den Simulationsaufbau. Bild 4 zeigt dabei neben einem grundlegenden Prozessmodell die maßgeblichen Prozessgrößen, die für die komplexen, hochdynamischen Temperaturfelder im Bauraum verantwortlich sind.
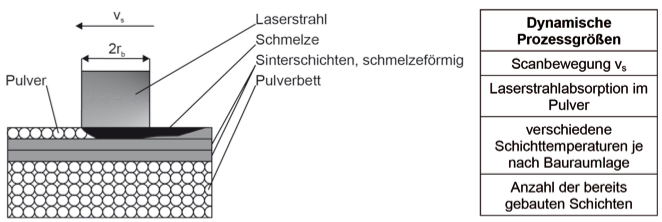
Bild 4: Dynamische Prozessgrößen im Prozessmodell des selektiven Lasersinterns
Bisherige Modelle zur numerischen Beschreibung des selektiven Lasersinterns bilden z.T. nicht alle dynamischen Teilprozesse in einem Modell ab. Tabelle 1 zeigt einen Vergleich verschiedener etablierter Simulationsmodelle und die darin abgebildeten Teilprozesse.
|
Modell |
Anzahl der gebauten Schichten |
Scanbewegung |
Laserabsorption |
|
Alscher [6], Nöken [7], Keller [8] |
1 |
Nein |
Einzelpunktlasten |
|
Childs [9], Steinberger [10] |
>1 |
Ja |
Bauen einer Kontur |
Tabelle 1: Vergleich etablierter Simulationsmodelle
Für den Aufbau eines eigenen Simulationsmodells ist es deshalb unerlässlich möglichst alle in Bild 4 gezeigten dynamischen Prozessgrößen abzubilden. Hauptbestandteil der Simulation ist deshalb die Modellierung einer bewegten Wärmequelle.
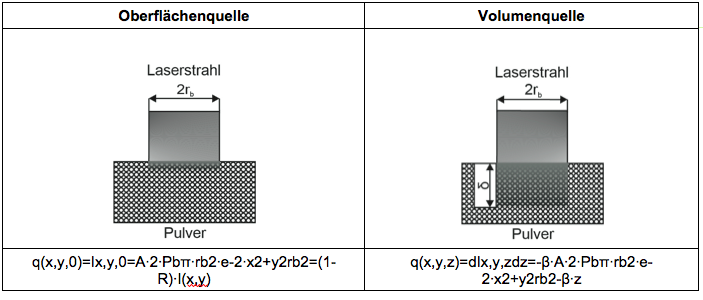
Je nach verwendetem Material unterscheidet sich die Absorption der Laserstrahlung im Pulver grundlegend voneinander. In Metallpulvern erfolgt eine oberflächennahe Absorption der Laserstrahlung, während hingegen bei teilkristallinen Thermoplasten eine Strahlungsabsorption entlang der Schichtdicke (Volumenquelle) erfolgt. Je nach Art der Wärmequelle unterscheidet sich die mathematische Formulierung. Tabelle 2 zeigt eine Gegenüberstellung beider Wärmequellformen und deren mathematische Beschreibung.
Der Simulationsablauf ist am realen Produktionsprozess orientiert. Demzufolge unterteilt sich der Gesamtprozess der Bauteilgenerierung in die drei Teilprozesse der Vorwärmphase, der Bauphase und der Abkühlphase. Das bedeutet, dass drei unabhängige Simulationsabläufe erstellt wurden, zwischen denen die berechneten oder vorgegebenen Temperaturverteilungen übergeben werden.
Ziel ist es anhand des Simulationsmodells grundlegende Aussagen über den Einfluss der im Volumenquellterm (vgl. Tabelle 2) enthaltenen Größen sowie über den Einfluss verschiedener Prozessgrößen (z.B. Laserleistung) und thermischer Materialwerte insbesondere der Wärmeleitfähigkeit auf das Berechnungsergebnis treffen zu können. So wird eine Ausgangsbasis geschaffen, um gezielt Experimente zur Modellierung der signifikanten Eingangsgrößen durchzuführen. Tabelle 3 zeigt die analysierten Eingangsgrößen.
|
Art |
Parameter |
Maximalwert (+1) |
Minimalwert (-1) |
|
Prozess-/Materialgrößen |
Laserleistung Pb |
10 W |
5 W |
|
Art der Wärmequelle |
Oberflächenquelle |
Volumenquelle |
|
|
Kornradius |
50 µm |
25 µm |
|
|
Wärmeleitfähigkeit |
0,054 W/(mK) |
0,027 W/(mK) |
|
|
optische Materialwerte |
Absorptionsgrad A |
66 % |
33 % |
|
Absorptionskoeffizient β (=1/Partikeldurchmesser [7]) |
1/(25 µm) |
1/(50 µm) |
Tabelle 3: Analysierte Größen innerhalb einer Parameterstudie
Die Eindringtiefe der Wärme in die Pulverschicht ist ein entscheidender Parameter zur Beurteilung der Anbindung an das darunterliegende Pulver. Folglich wird die Wärmeeindringtiefe als Zielgröße der Parameterstudie verwendet. Zur Erfassung der Wärmeeindringtiefe wird die Temperatur an der Schichtunterseite mittels FEM berechnet. Je höher diese Temperatur ist, desto tiefer ist die Laserstrahlung in den teilkristallinen Thermoplasten penetriert.
Im Folgenden wird ausschließlich die zum Zeitpunkt der Belichtung erreichte Temperatur Tu an der Schichtunterseite (vgl. Bild 5) als Ergebnisgröße betrachtet.
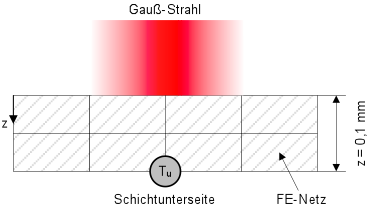
Bild 5: Position der Ergebnisgröße Tu in der Pulverschicht
Bild 6 zeigt die quantifizierten Effekte der in Tabelle 3 aufgeführten Prozess- und Materialgrößen auf die, an der Schichtunterseite, berechnete mittlere Temperatur Tu zum Zeitpunkt der Penetration (t=t0) durch den Laser.
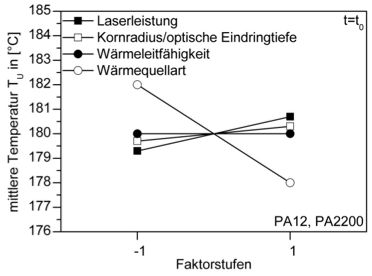
Bild 6: Effekte der Material-/Prozessgrößen auf die Wärmeeindringtiefe
In Tabelle 4 sind die einzelnen Einflüsse der Prozess-/Materialgrößen auf die Wärmeeindringtiefe detaillierter erläutert.
|
Verhalten der Zielgröße |
Erläuterung |
|
|
Laserleistung |
Eine erhöhte Laserleistung resultiert in einer höheren Wärmeeindringtiefe |
Ein höherer Wärmestrom auf Grund erhöhter Laserleistung hat bei gleicher optischen Eindringtiefe δ eine höhere Temperatur an der Schichtunterseite zur Folge |
|
Kornradius/optische Eindringtiefe |
Eine Erhöhung des Kornradius bewirkt eine gesteigerte optische Eindringtiefe [7] sowie eine höhere Sintertiefe [6] und folglich eine erhöhte Temperatur an der Schichtunterseite |
Ein höherer Kornradius bewirkt größere Hohlräume zwischen den Partikeln und eine geringere Packungsdichte der Schüttung; die Laserstrahlung kann folglich tiefer eindringen und es kommt zu einer höheren Temperatur an der Schichtunterseite |
|
Wärmeleitfähigkeit |
kein Effekt |
Direkt bei der Penetration steht bei Thermoplasten nicht ausreichend Zeit zur Verfügung für die langsam ablaufenden Wärmeleitvorgängen |
|
Wärmequellart |
Die Temperatur an der Schichtunterseite nimmt beim Wechsel von einer Volumen- hin zu einer Oberflächenquelle ab |
Die Volumenquelle penetriert im Gegensatz zur Oberflächenquelle das Pulver; bei der Oberflächenquelle erfolgt die Erwärmung der Schichtunterseite durch Wärmeleitung von der Oberfläche in die Tiefe; diese Wärmeleitung erfolgt sehr langsam; folglich ist die Temperatur an der Schichtunterseite bei der Volumenquelle höher |
Tabelle 4: Effekte der Material-/Prozessgrößen auf die Wärmeeindringtiefe direkt bei Einwirken eines Laserstrahls
Der Einfluss der optischen Eigenschaften eines Pulvers auf die berechnete Wärmeeindringtiefe wird in Bild 7 dargestellt.
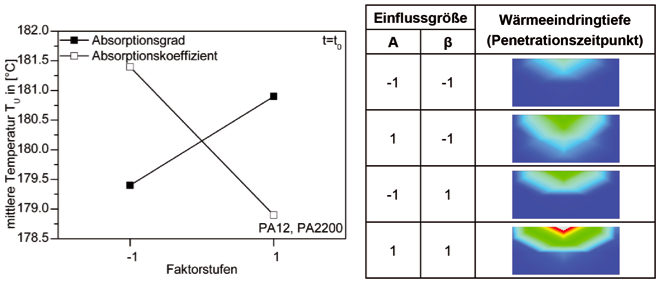
Bild 7: Effekt der optischen Materialeigenschaften auf die Wärmeeindringtiefe
Beide optischen Parameter verhalten sich genau invers zueinander, wie die Erläuterung der Effekte in Tabelle 5 zeigt.
|
Verhalten der Zielgröße |
Erläuterung |
|
|
Absorptionsgrad |
Eine Erhöhung des Absorptionsgrads erhöht die Wärmeeindringtiefe |
Ein erhöhter Absorptionsgrad kommt einer Vergrößerung der Laserleistung gleich, da mehr Laserstrahlung in die Pulveroberfläche eingekoppelt wird; in der Folge liegt insgesamt das Temperaturniveau im Prozess höher |
|
Absorptionskoeffizient |
Eine Erhöhung des Absorptionskoeffizienten bedingt eine Erniedrigung der Wärmeeindringtiefe |
Der erhöhte Absorptionskoeffizient bedingt als Reziprokwert der optischen Eindringtiefe eine niedriges Eindringen der Laserstrahlung in das Pulver [7] |
Tabelle 5: Einfluss der optischen Materialeigenschaften auf die Wärmeeindringtiefe
Es wurde ein erster Ansatz zur Modellierung des Lasersinterprozesses von thermoplastischen Werkstoffen durchgeführt. Wesentlich für die Definition des Materialmodells sind die Analyse von signifikanten Einflussfaktoren und die Ableitung realitätsnaher Stoffwerte. Anhand eines vollfaktoriellen Versuchsplans durchgeführte Simulationen zeigen, dass die Wärmeleitfähigkeit direkt bei der Belichtung keinen Effekt auf die Temperaturverteilung im Pulver ausübt. Dies legt die Vermutung nahe, dass sich erst mit zunehmender Prozesszeit nach der Belichtung eines Betrachtungspunktes die Wärmeleitung als Verlustwärmestrom auf die Temperaturverteilung an diesem Punkt auswirkt. Die Wärmeleitung unterliegt demzufolge einer starken Zeitabhängigkeit innerhalb des Simulationsmodells. Diesen Sachverhalt bestätigen die unterschiedlichen Bauteileigenschaften von Sinterteilen aus gefüllten, bzw. ungefüllten Thermoplastpulvern. Von großer Bedeutung für die Abbildung des Laserenergieeintrags ist der verwendete Wärmequellterm. Eine programmiertechnisch einfach umzusetzende Oberflächenquelle erweist sich als ungeeignet zur adäquaten Abbildung der Energieeinbringung in das Pulverbett eines teilkristallinen Thermoplasten. Der alternativ verwendete Volumenquellterm, welcher extern als User-Subroutine in FORTRAN® programmiert wurde, basiert auf dem Lambert-Beerschen-Absorptionsgesetz. Ausgehend von diesem Vollumenquellterm werden anhand von Parameterstudien die Eingangsgrößen im Term identifiziert, die das Berechnungsergebnis signifikant beeinflussen. So können gezielt und effizient Versuchsreihen zur experimentellen Bestimmung und darauffolgenden Modellierung der einflussreichsten Eingangsgrößen durchgeführt werden. Die optischen Kenngrößen Absorptionsgrad und Absorptionslänge im Volumenquellterm stellen sich als entscheidende Einflussgrößen auf die mittels FEM berechnete Temperaturverteilung heraus, da sie maßgeblich die Größe des Energieeintrags durch den Laser in das Pulver determinieren. Folglich ist in zukünftigen Arbeiten eine exakte Modellierung dieser optischen Materialeigenschaften basierend auf experimentellen Erkenntnissen durchzuführen. Ein Ansatz kann eine Modifikation des Volumenquellterms darstellen, z.B. durch einen individuell für jedes zu simulierende Material abgeleiteten Absorptionskoeffizienten. Erste Simulationsreihen mit einem modifizierten Absorptionskoeffizienten liefern gute Ergebnisse für eine invers-lineare Verknüpfung zwischen Absorptionskoeffizient und dem 1,5-fachen Partikeldurchmesser. Langfristig ist geplant auf dieser Basis den Lasersinterprozess simulieren zu können, um insbesondere einen tieferen Einblick in die ablaufenden Prozesse im Randbereich Pulver-Schmelze erhalten zu können.
Die Autoren danken der AiF (IGF 16111 N/2) für die finanzielle Unterstützung der Untersuchungen
[1] Wohlers, T.: Wohlers Report 2009 - Rapid Prototyping - State of the Industry, 2009.
[2] Rietzel, D., Drummer, D., Kühnlein, F.: "Investigation of the particular crystallization behaviour of semi-crystalline thermoplastic powders processed by selective laser sintering.," presented at the 3rd International Conference on Additive Technologies; DAAAM Specialized Conference, Nova Gorica, Slovenia, 2010.
[3] Rietzel, D., Kühnlein, F., Drummer, D.: Characterization of New Thermoplastics for Additive Manufacturing by Selective Laser Sintering SPE Proceedings ANTEC (2010)
[4] N.N.: "Generative Fertigungsverfahren," in Vorlesung Kunststofftechnik 1, Erlangen: Lehrstuhl für Kunststofftechnik (LKT), 2008.
[5] Drummer, D., Rietzel, D., Kühnlein, F.: Selektives Lasersintern von teilkristallinen Thermoplasten, RTejournal 6 (2009) S. 14
[6] Alscher, G.: Das Verhalten teilkristalliner Thermoplaste beim Lasersintern, Dissertation, Universität Essen, Aachen, 2000.
[7] Nöken, S.: Technologie des Selektiven Lasersinterns von Thermoplasten, Dissertation, Fakultät für Maschinenwesen, Rheinisch-Westfälische Technische Hochschule Aachen, 1997.
[8] Keller, B.: Grundlagen zum selektiven Lasersintern von Polymerpulver: Universität Stuttgart, 1998.
[9] Childs, T. H. C., Tontowi, A. E.: Selective laser sintering of a crystalline and a glass-filled crystalline polymer: experiments and simulations, School of Mechanical Engineering, University of Leeds, UK 215 Part B (2001) S. 1481-1494
[10] Steinberger, J.: Optimierung des Selektiven-Laser-Sinterns zur Herstellung von Feingußteilen für die Luftfahrtindustrie. Düsseldorf: VDI-Verl., 2001.
Prof. Dr.-Ing. Dietmar Drummer
Lehrstuhl für Kunststofftechnik
Friedrich-Alexander-Universität Erlangen-Nürnberg
Am Weichselgarten 9
91058 Erlangen
Email:
drummer@lkt.uni-erlangen.de
WEB:
www.lkt.uni-erlangen.de
Dipl.-Ing. Dominik Rietzel
Lehrstuhl für Kunststofftechnik
Friedrich-Alexander-Universität Erlangen-Nürnberg
Am Weichselgarten 9
91058 Erlangen
Email:
rietzel@lkt.uni-erlangen.de
WEB:
www.lkt.uni-erlangen.de
Dipl.-Ing. Maximilian Drexler
Lehrstuhl für Kunststofftechnik
Friedrich-Alexander-Universität Erlangen-Nürnberg
Am Weichselgarten 9
91058 Erlangen
Email:
drexler@lkt.uni-erlangen.de
WEB:
www.lkt.uni-erlangen.de