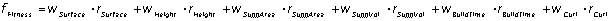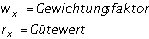Ermittlung optimaler Bauteilorientierung zur Verbesserung der Prozessplanung in der CAD/RP-Kette
© 2009 Stéphane Danjou; Lizenznehmer RTejournal, weitere Informationen sind zu finden unter: http://www.dipp.nrw.de/service/dppl/
urn:nbn:de:0009-2-22107
Zusammenfassung
Ein wesentlicher Einflussfaktor auf die Bauteilqualität und Prozessgüte bei der generativen Herstellung von Prototypen ist die Orientierung der Bauteile. So kann eine optimierte Ausrichtung den Treppenstufeneffekt (Staircasing) sowie den Curling-Effekt minimieren und somit die Oberflächenqualität bzw. die Bauteilgenauigkeit erhöhen oder die Berücksichtigung von Formtoleranzen (z.B. Rundheit) ermöglichen. Des Weiteren können verschiedene Bauteilausrichtungen unterschiedliche Ausführungen von Stützkonstruktionen bewirken und die Bauteilstabilität beeinflussen. Diese und ähnliche Wechselwirkungen gilt es bei der Auswahl einer geeigneten Bauteilorientierung für RP-Anwendungen zu berücksichtigen. Dieser Vortrag stellt ein generisches System vor, welches unter Berücksichtigung der genannten Einflussfaktoren sowie weiterer Effekte eine rechnergestützte Optimierung der Bauteilorientierung durchführt. Neben der weiterhin notwendigen Erfahrung der Anwender zur endgültigen Festlegung der fallabhängigen Bauteilausrichtung liefert das System Vorschläge auf Basis einer intensiven Geometrieanalyse, die eine entsprechende Datenaufbereitung im Rahmen der Prozessplanung unterstützen.
Abstract
In layered manufacturing, part orientation is a significant factor of influence on part and process quality. For instance, optimized part-building orientation can minimize the staircase effect as well as the curling effect and therefore increase surface quality and part accuracy respectively. Another advantage of optimized build direction is the possible consideration of form tolerances (e.g. circularity). Furthermore, different part orientations can lead to varying implementations of supports and influence part stability. These and related feedback effects have to be considered when selecting an appropriate part orientation for Rapid Prototyping applications. This paper presents a generic system to determine optimal part orientation in consideration of the mentioned factors of influence as well as related effects. In addition to further necessary experiences of the machine operators and service providers to finally set the case dependent part orientation, the introduced concept offers suggestions on the basis of an intensive geometry analysis. This can support data preparation within process planning.
Der Einsatz neuer Fertigungsverfahren gehört zu den Maßnahmen zur Verbesserung der Effizienz von Produktionsprozessen. Nicht unerwartet haben sich daher auch die Anwendungen der Rapid Technologie im Laufe der Zeit als Potenzialträger im modernen Produktentwicklungsprozess herauskristallisiert [1]. Auf Grund des Alleinstellungsmerkmals der nahezu werkzeuglosen generativen Bauteilherstellung ging in den letzten Jahren der Einsatz dieses Verfahrens weit über die Erzeugung physischer Prototypen (Rapid Prototyping – RP) hinaus. Die Weiterentwicklungen auf diesem Gebiet haben vielmehr dazu geführt, dass mit Hilfe der Rapid Technologie die schnelle Herstellung marktfähiger Produkte mit serienidentischen oder seriennahen Eigenschaften möglich ist (Rapid Manufacturing – RM) [2]. Einhergehend mit den Verfahrensverbesserungen (Material, Leistung, etc.) und der zunehmenden Vielseitigkeit steigt jedoch auch die Anzahl verfahrensspezifischer Wechselwirkungen und somit die Komplexität der Prozessvorbereitung. Während noch zahlreiche Einflussgrößen nur unzureichend bekannt sind, baut das Verfahrens-Know-how im Wesentlichen auf den zumeist langjährigen Erfahrungen der Anlagenhersteller und Anlagenbediener auf. Eine in Normen und Richtlinien festgehaltene Wissensbasis liegt bis dato nicht vor.
Wesentlicher Bestandteil der Prozessvorbereitung ist die geeignete Auswahl der Bauteilorientierung. Zahlreiche orientierungsabhängige Effekte wie der Treppenstufeneffekt oder auch Auswirkungen anisotroper Materialeigenschaften wie Festigkeit und Schrumpfverhalten des Materials müssen bei der Wahl der Bauteilausrichtung Berücksichtigung finden [3]. Dieser Vorgang gestaltet sich jedoch mit steigender Bauteilkomplexität schwieriger und macht in zunehmendem Maße ein computergestütztes Hilfsmittel zur Entscheidungsfindung notwendig.
Die Auswahlkriterien einer optimalen Orientierung richten sich maßgeblich nach dem Verwendungszweck (Geometrie-, Funktions-, Werkzeug-, serienidentischer Prototyp) des generativ herzustellenden Bauteils. Denn hierauf aufbauend gestaltet sich die Auswahl eines geeigneten Verfahrens und letztendlich des zu verwendenden Materials, das auf Grund seiner anisotropen Eigenschaften einen großen Einfluss auf die Bauteilausrichtung ausübt. Insbesondere eine inhomogene Temperaturverteilung, sowohl im Bauteil, als auch im gesamten Bauraum, kann zu ungewolltem Materialverzug und somit zu einer ungenügenden Maßhaltigkeit führen. In der Regel kann diesem Umstand bereits durch geeignete Prozessparameter (Leistung, Belichtung) und Baustrategien (z.B. Belichtungspfad, Schrumpfkompensation, etc.) sowie eine genaue Temperaturregelung im Bauraum entgegengewirkt werden [4]. Jedoch kann die Berücksichtigung potenzieller Temperaturgradienten bei der Festlegung der Bauteilorientierung hilfreich sein. Hierzu sind beispielsweise große Sprünge der Querschnittsflächen aufeinanderfolgender Schichten zu vermeiden. Ebenso neigen große Belichtungsflächen in Folge von Verzug zum Aufrollen (Curling), was durch leichte Neigung des Bauteils um wenige Grad zur Horizontalen verhindert werden kann.
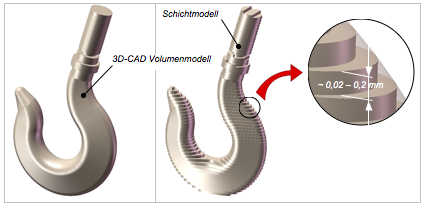
Ein weiterer entscheidender Einflussfaktor ist die gewünschte Bauteilqualität. Verfahrensbedingt können je nach Bauteilorientierung unterschiedliche Ausführungen von Stützkonstruktionen (Supports) notwendig sein, die eine mechanische oder chemische Nachbearbeitung (Post Processing) des Bauteils erfordern [5]. Gerade Funktionsflächen sollten derart berücksichtigt werden, dass in der gewählten Bauteillage die Kontaktfläche zu angreifenden Supports möglichst gering gehalten wird. Des Weiteren übt das Charakteristikum der generativen Fertigungsverfahren, der Treppenstufeneffekt (Stair Casing), eine große Wirkung auf die Qualität des Bauresultats aus. Dieser Effekt tritt verstärkt sowohl bei gewölbten als auch zur Bauplattform geneigten Flächen auf (siehe Abb. 1). Demzufolge ist eine Bauteilorientierung mit möglichst zur Schichtebene senkrecht angeordneten Flächen anzustreben.
Abb. 1: Treppenstufeneffekt infolge des Schichtbauprinzips
Neben diesen Kriterien gewinnt die Betrachtung der Wirtschaftlichkeit zunehmend an Bedeutung. Zusätzlich zu den Fixkosten (Investitions-, Personal-, Instandhaltungskosten, etc.) tragen die variablen Kosten (Material- und Betriebskosten) erheblich zu den Gesamtkosten bei. Somit gilt es bei der Orientierungsauswahl die Baukosten zu berücksichtigen, die sich sowohl in der Bauzeit und somit indirekt in der Bauhöhe, als auch in der Menge des verwendeten Materials widerspiegeln. Weitere Kosten verursachende Faktoren wie Vorbereitungs- und Einrichtzeiten oder auch Materialaufbereitung und Instandsetzung tragen als variable Kosten ebenfalls zur Änderung der Wirtschaftlichkeit bei, sind aber unabhängig von der Bauteilorientierung und finden demzufolge keine Berücksichtigung bei der Festlegung.
Die Berücksichtigung der vorgestellten Einflussfaktoren bei der Auswahl einer geeigneten Bauteilausrichtung im Rahmen der Prozessvorbereitung gestaltet sich ohne eine langjährige Erfahrung als äußerst schwierig, wenn nicht sogar unmöglich. Zum heutigen Zeitpunkt stehen dem Anwender zahlreiche Tools zur Unterstützung der Bauprozessplanung zur Verfügung, insbesondere für das Erzeugen von Supports, die Simulation der Schichtzerlegung (Slicing), die Bauraumaufteilung (Packing), usw. Allen Applikationen ist jedoch gemein, dass die Untersuchungen und Berechnungen eine festgelegte Bauteilorientierung voraussetzen. Dabei ist gerade auf Grund der zu erwartenden Verfahrensverbesserungen mit einem Anstieg der Komplexität des Prozesses zu rechnen. Dies erfordert computergestützte Berechnungsverfahren in Form einer multikriteriellen Optimierung, die das Wissen eines erfahrenen Anwenders niemals ersetzen, jedoch maßgeblich bei der Auswahl einer Orientierung unterstützen kann.
Neben der Kenntnis der Existenz Einfluss ausübender Faktoren ist das Greifbar-Machen, also die Zuordnung verarbeitbarer Kenngrößen, von entscheidender Bedeutung. Gerade die Quantifizierung der Bauteilqualität, welche zunächst lediglich ein Ausdruck subjektiver Wahrnehmung zu sein scheint, bedarf eines besonderen Augenmerks. Im Folgenden werden Ansätze für eine zahlenmäßige Erfassung der zuvor erläuterten Effekte vorgestellt. Dabei lassen sich die zu berücksichtigenden Effekte in drei Kategorien unterteilen: Qualität, Kosten und mechanisch-technologische Eigenschaften.
Die Bauteilqualität wird im Wesentlichen durch die Abbildungstreue des Schichtmodells gekennzeichnet. Abweichungen von der gewünschten Bauteilgeometrie verändern die Maßhaltigkeit und somit insgesamt die Bauteilqualität. Ein mögliches Maß hierfür ist die schichtweise ermittelte Volumendifferenz zwischen Soll-Geometrie und dem Schichtmodell. In der Regel repräsentiert ein 3D-CAD-Volumenmodell die Soll-Geometrie, wobei jedoch die Schichtgenerierung auf der Grundlage einer facettierten Darstellung (z.B. STL-Format) erfolgt und somit streng genommen das Facettenmodell die Eingangsgröße in der Prozessplanung darstellt (siehe Abb. 2a). Eine alternative Vorgehensweise ist die Schichterzeugung anhand des nativ vorliegenden 3D-CAD-Modells (Direct Slicing). Diese Methode findet jedoch derzeit kaum Anwendung.
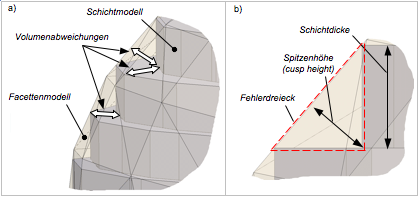
Abb. 2: Quantifizierung der Bauteilqualität a) Volumendifferenz; b) Fehlerdreieck
Auf Grund des erheblichen Rechenaufwands für eine schichtweise Ermittlung der Volumendifferenz kann alternativ der Ansatz zur facettenweisen Bestimmung der so genannten Spitzenhöhe (cusp height) angewendet werden. Dies ist die maximale Abweichung in einem gedachten Fehlerdreieck (vgl. Abb. 2b) einer Facette. Diese Art der Erfassung der Bauteilabweichung ist etwas ungenauer, da die Definition eines Fehlerdreiecks bei Änderungen des Neigungswinkels einer Facette innerhalb einer Schicht nicht immer eindeutig möglich ist. Dennoch gibt dieser Ansatz in angemessener Form Aufschluss über die zu erwartenden Formabweichungen von der Soll-Geometrie.
Ein weiterer die Qualität beeinflussender Faktor stellt die Temperaturverteilung im Bauteil dar. Ohne spezielle Software zur Simulation der Wärmeverteilung ist eine genaue Werterfassung nicht möglich. Jedoch gibt die Ermittlung großer Belichtungsflächen und großer aufeinanderfolgender Querschnittssprünge Anhaltspunkte über potenzielle Temperaturgradienten. Auch wenn in diesem Bereich noch Erfahrungswerte fehlen, kann dennoch diese Art der Quantifizierung für eine überschlägige Berechnung verwendet werden.
Einen zusätzlichen Beitrag zur Erfassung der Bauteilqualität liefert die Kenntnis des Flächeninhalts der von Supports betroffenen Flächen. Eine Minimierung dieses Flächeninhalts bei der Ermittlung optimaler Bauteilorientierung kann den erforderlichen Aufwand für das Post Processing herabsetzen [6]. Abb. 3 zeigt anhand eines Bauteils wie durch Veränderung der Orientierung angreifende Stützstrukturen aus einem hinsichtlich des Designs sensiblen Bereich (Gesichtspartie) in einen weniger kritischen Bereich (Hinterkopf) verlagert werden können.
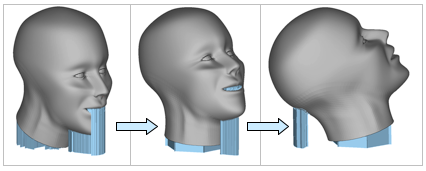
Abb. 3: Kontaktflächen zu Supports
Neben der Kenntnis der Kontaktflächen ist ebenfalls zur Minimierung des Aufwands für das Post Processing die Entfernbarkeit der Supports zu berücksichtigen. Die orientierungsabhängigen Ausführungen notwendiger Supports müssen nach dem Bauprozess entfernt werden können. Dies erfordert eine ausreichende Zugänglichkeit notwendiger Werkzeuge, so dass dieser Aspekt bereits bei der Festlegung der Orientierung mit einfließt.
Die orientierungsabhängigen Baukosten werden vorrangig durch den Materialaufwand und die benötigte Bauzeit festgelegt. Da in der Regel belichtetes Material nicht wiederverwendet werden kann, ist neben dem für die Erstellung der Bauteilgeometrie notwendigen Material ebenfalls der Materialaufwand für eventuell anfallende Stützstrukturen zu berücksichtigen. Dies hat zur Folge, dass bei der Festlegung der Bauteilorientierung ein Minimum an Supportvolumen anzustreben ist. Neben dem Materialaufwand stellt die Bauzeit einen signifikanten Kostenfaktor dar. Hier wird zwischen der Netto-Bauzeit des Bauteils und verfahrensspezifischen Nebenzeiten unterschieden. Nebenzeiten umfassen Zeiten der Vorbereitung (z.B. Einrichten, Aufheizen), des Post Processing (Nachvernetzen, Abkühlen, etc.) und des Finishing. Sie sind orientierungsunabhängig und können somit bei der Orientierungsoptimierung vernachlässigt werden. Die eigentliche Bauzeit in der Anlage setzt sich hauptsächlich aus den Belichtungs- und Beschichtungszeiten (Recoating) der einzelnen Schichten zusammen. Somit ergibt sich eine direkte Abhängigkeit zwischen Bauzeit und Anzahl der zu fertigenden Schichten. Da die Schichtanzahl sowie das Materialvolumen jedoch nicht getrennt voneinander berücksichtigt werden können, liefert die Kombination aus verfahrens- sowie materialabhängiger Volumenaufschmelzrate und anwendungsbedingter Beschichtungszeit einen guten Anhaltspunkt. Übliche Werte für die Aufschmelzrate bewegen sich in einem Bereich von 1,5 – 4 mm³/s.
Neben den Qualitäts- und Kostenfaktoren ergeben sich ebenfalls Abhängigkeiten zwischen der Orientierung des Bauteils im Bauraum und den mechanisch-technologischen Eigenschaften. So ist bei generativ hergestellten Bauteilen die Festigkeit innerhalb einer Schicht stets größer als zwischen den Schichten. Entsprechend dem Einsatzzweck des generativ herzustellenden Bauteils und den daraus resultierenden Beanspruchungsformen sollte demzufolge die Bauteilorientierung auch hinsichtlich der Richtungsabhängigkeit der Festigkeit ausgewählt werden.
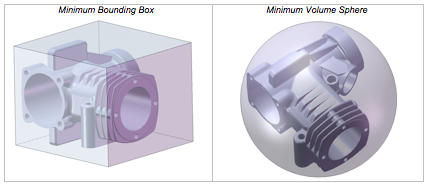
Die vorliegende Optimierungsaufgabe entspricht einer Multiziel-Optimierung. Aktuelle Forschungsaktivitäten an der Universität Duisburg-Essen beschäftigen sich mit der Umsetzung eines Optimierungsalgorithmus zur Ermittlung optimierter Bauteilorientierung unter Berücksichtigung der vorgestellten Kriterien. Die programmiertechnische Umsetzung zur Erfassung der Optimierungskriterien erfolgte im Wesentlichen auf der Grundlage ausgewählter Werkzeuge aus dem Bereich der Algorithmischen Geometrie (auch bekannt unter Computational Geometry) [7]. So werden beispielsweise zur Ermittlung der Minimal- und Maximalabmessungen des Bauteils Algorithmen zur Berechnung verschiedener Umhüllenden verwendet (siehe Abb. 4).
Abb. 4: Umhüllende zur Ermittlung von Extremabmaßen
Des Weiteren basiert die Berechnung zahlreicher Kennwerte auf der Auswertung des Facettenmodells bzw. der konvexen Hülle, welche als Teilmenge aller Facetteneckpunkte den Rechenaufwand für einige Algorithmen erheblich reduziert. Auf Grund des schichtenabhängigen Charakters einiger Einflussfaktoren auf die optimierte Bauteilausrichtung wird in jeder analysierten räumlichen Lage die Schichtengenerierung simuliert. Die so ermittelten Schichtinformationen (z.B. Querschnittsfläche, Volumen, etc.) dienen der Kennwertermittlung, insbesondere zur Quantifizierung der Bauteilqualität.
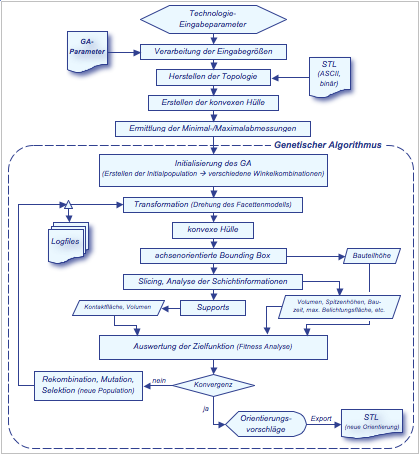
Das mit Hilfe der Programmiersprache C++ umgesetzte Konzept der Multizieloptimierung bedarf erheblicher Rechenleistung, wenn die Auflösung des Wertefelds (mögliche Drehwinkel räumlicher Drehung) mit 1° angesetzt wird. Dies würde zu 64.800 (360 x 180) Kombinationen führen, so dass hier der Einsatz eines Genetischen Algorithmus (GA) zielführender erscheint. Als ein wichtiger Vertreter der heuristischen Algorithmen lässt sich mit einem GA im Gegensatz zu klassischen Suchstrategien eine geschlossene Lösung für das vorliegende Optimierungsproblem effizienter berechnen [8]. Der Ablauf der Multiziel-Optimierung lässt sich Abb. 5 entnehmen.
Abb. 5: Ablaufschema der Orientierungsoptimierung
Die Orientierungsoptimierung gestaltet sich im Wesentlichen durch iteratives Ändern der räumlichen Lage des Bauteils sowie die Berechnung aller orientierungsabhängigen Kennwerte. Damit die Priorität des Bauprozesses (Qualität Wirtschaftlichkeit) angemessene Berücksichtigung findet, werden die orientierungsabhängigen Kenngrößen mit Gewichtungsfaktoren versehen. Die gewichteten Gütefaktoren bilden zusammen eine für den GA notwendige Zielfunktion, anhand derer ein Lösungskandidat bewertet wird. Lösungen mit besseren Zielfunktionswerten werden mit einer höheren Wahrscheinlichkeit als „überlebendes Individuum“ ausgewählt. Hier kennzeichnet die Zielfunktion die so genannte Fitness einer Orientierung:
|
|
Solange ein entsprechendes Abbruchkriterium (z.B. Konvergenz der Fitnessfunktion oder max. Anzahl an Iterationsschritten bzw. Generationen) nicht erfüllt wird, werden mit Hilfe der genetischen Operatoren (Selektion, Rekombination und Mutation) neue Individuen einer Population generiert, also neue Winkelkombinationen als Lösungskandidaten ausgewählt. Die auf diese Weise sukzessiv ermittelten Orientierungen lassen sich zur Visualisierung als Facettenmodell (STL) ausgeben.
Das vorgestellte Konzept zur Optimierung der Bauteilorientierung berücksichtigt eine Vielzahl an Einflussfaktoren und liefert eine frei wählbare Anzahl an Lösungsvorschlägen der Optimierungsaufgabe als Hilfsmittel für die Auswahl der Ausrichtung. Neben den hier vorgestellten Abhängigkeiten existieren weitere Effekte, die es in zukünftigen Entwicklungen zu berücksichtigen gilt und somit die Aussagekraft der Berechnungsergebnisse weiter erhöhen. Auf Grund der Komplexität der Orientierungsauswahl ist jedoch zunächst die Kenntnis der ausschlaggebenden Effekte und Wechselwirkungen von grundlegender Bedeutung. Abb. 6 veranschaulicht anhand einer Beispieloptimierung die mit der bisherig entwickelten Applikation erzielbaren Ergebnisse.
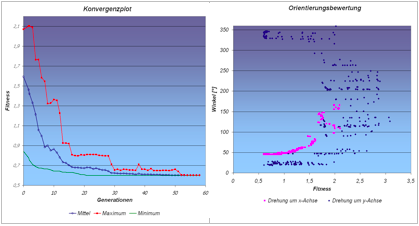
Abb. 6: Beispieloptimierung: Konvergenzplot und Orientierungsbewertung
Im vorliegenden Beispiel wurde die Orientierung eines Bremshebels optimiert. Anhand des Konvergenzplots (Abb. 6, linke Seite) lässt sich erkennen, dass im Verlaufe der Optimierung, also mit steigender Anzahl an Generationen, der Fitnesswert gegen ein Minimum konvergiert. Da der Fitnesswert die Bewertung eines Individuums (eine möglich Orientierung) hinsichtlich aller orientierungsabhängigen Effekte darstellt, wird insgesamt die Bauteilausrichtung optimiert. Die Orientierungen mit der kleinsten Fitness repräsentieren das beste Ergebnis. Abb. 6 (rechte Seite) zeigt die in Rotationswinkeln ausgedrückten Orientierungen mit den entsprechenden Fitnesswerten. Hier ist zu erkennen, dass eine Rotation von ca. 45° um die x-Achse mit anschließender Rotation um etwa 20° oder 340° um die y-Achse eine mögliche Lösung der Optimierungsaufgabe ist. Abb. 7 zeigt die dazugehörige Orientierung des Bauteils im Bauraum.
Abb. 7: Vorschlag für eine optimierte Bauteilorientierung
Es ist jedoch zu beachten, dass die ermittelten Orientierungen als Vorschläge und Hilfsmittel für die Entscheidungsunterstützung und nicht als absolute Ergebnisse anzusehen sind. Denn solange Konstruktionsabsichten, Funktionsflächen oder Besonderheiten in der Gestaltung nicht in einer entsprechenden Datenschnittstelle festgehalten werden können [9,10] und somit eine automatische Auswertung verhindern, bestimmt das Wissen eines erfahrenen Anwenders über die endgültige Festlegung der Bauteilorientierung.
Die Arbeiten waren Bestandteil des Forschungsvorhabenen Nr. 15351 BG, das im Rahmen der industriellen Gemeinschaftsforschung (IGF) vom Bundesministerium für Wirtschaft und Technologie über die AIF finanziert wurde.
[1] Birke, C.: Der Einsatz von Rapid-Prototyping-Verfahren im Konstruktionsprozess. Diss., Univ. Magdeburg, Institut für Maschinenkonstruktion, Magdeburg, 2002.
[2] Zäh, M. F.; Reinhart, G.: Rapid Manufacturing. - erfolgreich produzieren durch innovative Fertigung. Augsburg, München: Utz, 2007.
[3] Bablani, M.; Bagchi, A.: Quantification of Errors in Rapid Prototyping Processes and Determination of Preferred Orientation of Parts. Transactions of the North American Manufacturing Research Institution of SME, 1995, S. 319-324.
[4] Gebhardt, A.: Generative Fertigungsverfahren. - Rapid Prototyping - Rapid Tooling - Rapid Manufacturing. 3. Aufl., München: Hanser, 2007.
[5] Kim, H.; Lee, S.: Reduction of Post-Processing for Stereolithography Systems by Fabrication-Direction Optimization. In: Computer-Aided Design, Bd. 37 (2005), S. 711-725.
[6] Schwerdt, J.; Smid, M.; Janardan, R.; Johnson, E.: Protecting Critical Facets in Layered Manufacturing. In: Computer-Aided Design, Bd. 35 (2003), Nr. 7, S. 647-657.
[7] Klein, R.: Algorithmische Geometrie: Grundlagen, Methoden, Anwendungen. Springer, 2005.
[8] Weicker, K.: Evolutionäre Algorithmen. BG Teubner Verlag, 2007.
[9] Danjou, S.; Köhler, P.: Vorbereitung von CAD-Konstruktionsdaten für den RP-Einsatz – eine Schnittstellenproblematik. Rapid.Tech - Anwendertagung und Fachausstellung für Rapid-Technologie, Erfurt, 2008.
[10] Danjou, S.; Köhler, P.: Bridging the Gap between CAD and Rapid Technologies – Exigency of Standardized Data Exchange. Proceedings of the 12th European Forum on Rapid Prototyping, Ecole Centrale Paris, 2008.
Dipl.-Ing. Stéphane Danjou
Universität Duisburg-Essen
Institut für Produkt Engineering / Rechnereinsatz in der Konstruktion
Lotharstraße 1
47057 Duisburg / Germany
Tel.: +49 203/379-3935
Fax: +49 203/379-4379
Email:
stephane.danjou@uni-due.de
WEB :
www.uni-due.de/cae
Prof. Dr.-Ing. Dipl.-Math. Peter Köhler
Universität Duisburg-Essen
Institut für Produkt Engineering / Rechnereinsatz in der Konstruktion
Lotharstraße 1
47057 Duisburg / Germany
Tel.: +49 203/379-2790
Fax.: +49 203/379-4379
Email:
peter.koehler@uni-due.de
WEB:
www.uni-due.de/cae