Untersuchung und Simulation der Energieeinkopplung bei Metall verarbeitenden generativen Verfahren

Neben konventionellen, spanend und elektrochemisch abtragenden Fertigungstechnologien etablieren sich insbesondere in den letzten Jahren generative Verfahren auf dem Markt ¹ . Diese neuartigen Verfahren lassen sich grundlegend durch schichtweisen Aufbau und partielles Aufschmelzen definierter Pulverbereiche charakterisieren. Basierend auf der Verarbeitung polymerer Kunststoffe stellen diejenigen generativen Technologien, welche im Gegensatz zu früheren Entwicklungen inzwischen hochenergetische Energiequellen (Laser- und Elektronenstrahl) für die Verfestigung verschiedenster metallischer Legierungen nutzen, eine wirtschaftliche Alternative zu konventionellen Fertigungsverfahren dar ² . Signifikante Vorteile sind neben der erreichbaren Kosteneffizienz und kurzen Herstellzeiten auch der mögliche Verzicht auf aufwändige Datenexporte in Form von CAD-CAM-Schnittstellen. Wesentliche Einsatzfelder Metall verarbeitender Technologien sind sowohl Werkzeuge für die Herstellung von Kleinserien im Spritzgießen (Rapid Tooling) als auch die unmittelbare Realisierung von Produkten für den Endkunden (Rapid Manufacturing) ³ . Generative Fertigungstechnologien eignen sich daher aufgrund der nahezu gegebenen Kostenunabhängigkeit vom Grad der Produktkomplexität in idealer Weise für die wirtschaftliche Umsetzung von Mass Customization ⁴ .

Neben Laserstrahl-basierten Verfahren, wie beispielsweise Selective-Laser-Melting (SLM) oder Direct-Metal-Laser-Sintering (DMLS) existieren speziell im Bereich der Forschung Ansätze, die umfangreichen Vorteile des Elektronenstrahls für die generative Fertigung zu nutzen. Infolge der erhöhten Leistungsdichte und durch die hochflexible, schnelle Ablenkung mit Hilfe von elektromagnetischen Linsen sind weit reichende Potenziale dieser Energiequelle, speziell für die generative Fertigung, erkennbar ⁵ , ⁶ , ⁷ , ⁸ .

Die vorliegende Arbeit beschäftigt sich mit der Analyse auftretender physikalischer Wirkmechanismen der Elektronenstrahl basierten, generativen Fertigung. Speziell die elektromagnetische Abstoßung zwischen geladenen Teilchen und Pulverpartikeln stellt in diesem Zusammenhang einen wesentlichen Aspekt dar. Im Anschluss daran werden Aspekte der Energieeinkopplung betrachtet und mit Hilfe eines thermischen Simulationsmodells auf Basis der Finite-Elemente-Methode (FEM) modelliert. Durch die Auswertung des resultierenden instationären Temperaturfelds sollen Aussagen über die erzielbare Qualität einzelner Pulverschichten abgeleitet und mit Hilfe realer Versuche validiert werden.

Der Elektronenstrahl unterscheidet sich vom Laserstrahl grundsätzlich durch drei physikalische Kriterien. Zum einen besteht er als Korpuskularstrahl gegenüber der elektromagnetischen Welle des Lasers aus massebehafteten, geladenen Elementarteilchen. Zum anderen zeichnet er sich durch einen hohen Wirkungsgrad bei nahezu unbegrenzt hoher Leistung und die fast trägheitslose Ansteuerbarkeit von Strahlauftreffpunkt, Fokuslage und Strahlstrom aus ⁹ . Daraus resultieren für das Elektronenstrahlsintern eine Vielzahl prinzipbedingter Vorteile. Neben einer hohen Baugeschwindigkeit sind die Möglichkeit zur Verwendung hochschmelzender bzw. reaktiver Legierungen, sowie die hohe erreichbare Dichte des entstehenden Werkstoffgefüges zu nennen ⁵ .

Die wirtschaftliche Einsetzbarkeit des Elektronenstrahls für die generative Fertigung erfordert jedoch die Beherrschbarkeit neuartiger Prozessphänomene, wie das so genannte Verblasen. Die in Abbildung 1 dargestellten Aufnahmen einer Hochgeschwindigkeitskamera zeigen dieses Phänomen, bei dem sich Pulver unter Beaufschlagung mit dem Elektronenstrahl sofort explosionsartig ausbreitet, ohne dass thermische Energie in den Werkstoff übertragen wird.

Abbildung 1: Aufnahmen des Verblasens mit einer Hochgeschwindigkeitskamera ⁸

Hierbei erfolgte eine Elektronenbestrahlung des Metallpulvers mit einer Leistung von 400 W. Dieses Ausbreiten des Pulvers konnte unter anderem durch ein indirektes Vorheizen über die Erwärmung der umliegenden Metallplatte minimiert werden ⁸ . In Vergleichsversuchen wurde dieser Effekt beim Laserstrahlsintern mit einem 2 kWFestkörperlaser von metallischem Pulver nicht festgestellt. Der Effekt des Verblasens ist daher ursächlich auf die geänderten physikalischen Wirkprinzipien des Elektronenstrahls zurückzuführen. In Vorversuchen wurde erkannt, dass das verwendete Stahlpulver nahezu elektrisch isolierende Eigenschaften besitzt. Die Kontaktflächen der Körner sind derart klein, dass kein messbarer Strom fließt. Erst mit steigender Temperatur nähert sich die elektrische Leitfähigkeit des Pulvers dem Kennwert von Vollmaterial an, da durch die Ausbildung erster Sinterhälse eine leitende Verbindung hergestellt wird und die eingebrachte Ladung an die Erdung abgeführt werden kann. Sinterhälse entstehen zwischen den einzelnen Partikeln durch die angestrebte Reduktion der Grenzflächenenergie als Vorstadium im Sinterprozess. Bis zu diesem Zeitpunkt sind alle Partikel im Pulverbett durch die Beaufschlagung mit dem Elektronenstrahl elektrisch negativ geladen und stoßen sich somit gegenseitig ab, wodurch es zur beschriebenen explosionsartigen Verteilung der Pulverpartikel kommt. Ausgehend von der Coulomb-Kraft, die zwischen zwei Ladungen auftritt, kann die Auswirkung dieses Effektes abgeschätzt werden. Die abstoßende Kraft pro Partikel ist gegenüber der Gewichtskraft pro Partikel von etwa 1,08·10-9 N um ca. ein 1000 faches größer. Daher bestätigt sich die Annahme, dass die elektrische Aufladung die signifikanteste Ursache für den Effekt des Verblasens darstellt ⁶ .

Die EBS Technologie basiert analog zum SLM Prozess auf dem vollständigen Aufschmelzen einzelner Pulverbereiche und beinhaltet im Vergleich zu Sinterverfahren, wie SLS dadurch weitere Herausforderungen, welche zur Beherrschung des Prozesses gelöst werden müssen. So führt der zum Schmelzen des Metallpulvers notwendige Energieeintrag zu hohen Temperaturgradienten in der Pulverschicht. In der Folge werden hohe Eigenspannungen induziert, die zu Verzug und Delamination führen ¹⁰ . Die Existenz eines Schmelzbades erweitert die Anforderungen an einen kontrollierten Prozess zunehmend, da Effekte wie Oberflächenspannung und Strömung des Schmelzbades die Qualität der Schichtbildung beeinflussen.

Ein wesentlicher Aspekt zur Optimierung der Energieeinkopplung ist die Wahl einer adäquaten Scanstrategie ⁷ , ¹⁰ , um die maximal auftretende Temperaturdifferenz,bezogen auf die zu verfestigende Pulverschicht, zu minimieren. Da die EBSTechnologie eine Vielzahl von variablen Parametern beinhaltet, die den Energieeintrag in Höhe und Verteilung beeinflussen, ist es unabdingbar, numerische Simulationsmethoden zur Auswahl von verwendeten Scanstrategien einzusetzen.
Zur Untersuchung unterschiedlicher Belichtungsstrategien werden anwendungsbezogene thermische Simulationsberechnungen durchführt. Das zugrunde liegende Modell basiert auf der FEM und berücksichtigt die Translation eines konusförmigen mathematischen Wärmequellenmodells mit gaußförmiger Intensitätsverteilung (vgl. Abbildung 3). Innerhalb dieses Modells wurden Algorithmen hinterlegt, die eine Variation der maßgebenden Prozessparameter Strahlleistung, Scangeschwindigkeit und hatch-Abstand gewährleisten. Der hatch-Abstand bezeichnet in diesem Zusammenhang den senkrechten Abstand paralleler Belichtungslinien. Die Berechnungen konzentrieren sich auf die Vorhersage des instationären Temperaturfelds einzelner Schichten infolge der Belichtung definierter quadratischer Bereiche. Von wesentlicher Bedeutung ist dabei die sukzessive, partielle Anpassung temperaturabhängiger Materialkennwerte. Dies beinhaltet insbesondere ein Umschalten zwischen pulverund festkörperbezogenen Daten bei Erreichen der Schmelztemperatur. Die erhöhte Wärmeleitfähigkeit einzelner Teilbereiche trägt in der Folge signifikant zu einem beschleunigten Wärmetransport bei.

Durch die Auswertung der Simulationsergebnisse werden wesentliche Zusammenhänge in Form von Skalierungsfaktoren zwischen den Parametern Strahlleistung, Ablenkgeschwindigkeit und hatch-Abstand erwartet. Die Korrelationen werden wiederum als Eingangsgröße für experimentelle Versuchsreihen genutzt, um die numerischen Berechnungsergebnisse zu validieren. Die Zielsetzung besteht zusammenfassend darin, durch thermische Simulation künftig maßgebende Parameterzusammenhänge vor Beginn des Bauprozesses zu generieren, die Rückschlüsse auf die zu erwartende Prozesssicherheit und Bauteilqualität zulassen.

Die wesentliche Aufgabe der thermischen, makroskopischen Struktursimulation besteht in der hinreichend genauen Energieeinkopplung in den Pulverwerkstoff. Korrelierende physikalische Vorgänge und entsprechende Prozessparameter werden in Form eines mathematischen Wärmequellenmodells, das einzelne Kenngrößen implizit beinhaltet, in abstrahierter Weise abgebildet. Aus diesem Grund können reale Prozessparameter in umgekehrter Weise nicht unmittelbar aus den eingestellten Simulationsparametern extrahiert werden. Demgegenüber bietet die numerische Simulation aufgrund der Berücksichtigung maßgebender physikalischer Effekte jedoch die Möglichkeit, realitätsnahe Skalierungsfaktoren für den späteren Bauprozess zu bestimmen. Für die Modellierung der Energieeinkopplung des Elektronenstrahls im Sinterprozess wird ein gaußverteilter Konus zugrunde gelegt, der sich für die realitätsnahe Beschreibung des resultierenden Schmelzbades einzelner Spuren eignet. Ein hoher Übereinstimmungsgrad zwischen Simulation und Realität konnte bereits durch frühere Untersuchungen nachgewiesen werden ⁷

Für die Realisierung von Flächenbelichtungen sind reale Scanmuster, konsistierend aus einzelnen Spuren in Form entsprechender x- und y-Vektoren, in die Berechnung zu integrieren. Durch das Einlesen entsprechender Koordinaten werden essenzielle Prozessparameter, wie hatch-Abstand oder Abmessungen der zu belichtenden Fläche implizit vorgegeben und dadurch die notwendige so genannte weldline generiert. Die vorliegenden Untersuchungen basieren auf so genannten Schachbrettbelichtungen mit einer Elementkantenlänge von 2,0 mm. Ein wesentliches Differenzierungskriterium beschreibt der zugrunde liegende hatch-Abstand, d. h. der Abstand zwischen einzelnen Belichtungsspuren. Dadurch kann die eingebrachte Flächenenergie variiert werden. Die Reihenfolge der Belichtung einzelner Scanvektoren orientiert sich an der zeitlichen Abfolge realer Scanmuster. Aus diesem Grund werden zunächst die x-hatches sequenziell belichtet, bevor die vorliegenden y-hatches durchlaufen werden. Innerhalb einzelner hatches liegen Umkehrpunkte vor, d. h. die Belichtungsrichtung wechselt beim Übergang zwischen aufeinander folgenden Spuren. Abbildung 2 zeigt die Belichtungsmuster, welche in der thermischen Simulation untersucht wurden.

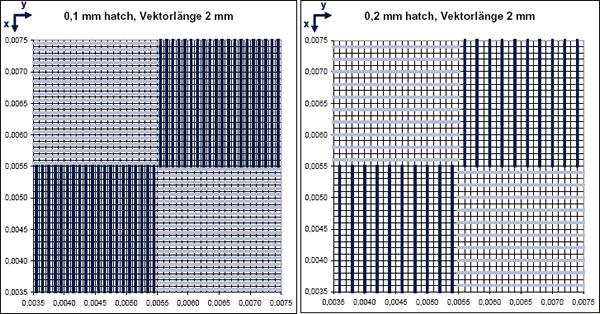
Abbildung 2: Flächenbelichtungsmuster für die thermische Berechnung

Die Wechselwirkung zwischen Elektronenstrahl und Metallpulver (1.2343) wird durch die mathematisch abstrahierte Lasteinbringung auf definierte Elemente gewährleistet. Während der Translation des Konus (vgl. Abbildung 3), der eindeutig durch die beiden Konusradien a und b, die Schichtdicke c sowie durch den Konuswinkel α festgelegt ist, werden exakt Elemente, deren Schwerpunkt innerhalb des bewegten Konus liegt, selektiert. Abhängig von Eindringtiefe des Strahls wird auf diese Elemente eine gaußverteilte Intensitätsverteilung aufgebracht, die mit zunehmender Tiefe um einen linearen Skalierungsfaktor abnimmt. Durch die Energieeinkopplung in das Pulverbett entstehen hohe Temperaturgradienten zur Umgebung, die durch Strahlungseffekte Berücksichtigung finden.

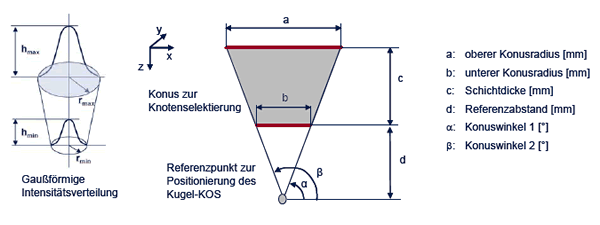
Abbildung 3: Mathematisches Wärmequellenmodell – Intensitätsverteilung und Parameter zur Knotenselektion für die Energieeinbringung ⁷

Im Folgenden werden unterschiedliche Belichtungsmuster auf Basis der hatch-Abstände 0,1 mm und 0,2 mm mit Hilfe des Simulationsmodells analysiert. Die Zielsetzung dieser Versuchreihen besteht darin, eine fundierte Korrelation zwischen den Parametern Strahlleistung und Ablenkgeschwindigkeit für variierende Scanmuster bei der gleichen eingebrachten Flächenenergie zu eruieren. Insbesondere soll durch numerische Berechnung gezeigt werden, dass auf Grund der instationären physikalischen Effekte keine Vorgabe konstant bleibender Skalierungsfaktoren zwischen den betrachteten Parametern gewährleistet ist. Zunächst wurden die Prozessparameter und Randbedingungen der thermischen Berechnung für den hatch-Abstand 0,1 mm auf Basis der Vorwärmtemperatur 800° C dahingehend kalibriert, dass sich ein idealisiertes, homogenes Schmelzbad, sowohl am Ende einzelner Belichtungsfelder als auch nach Beendigung einer vollständigen Belichtungsfigur ergibt. Abbildung 4 zeigt die berechneten Temperaturfelder für die Belichtung entsprechend Abbildung 2 links, d. h. es wurde zunächst in der x- Koordinatenrichtung belichtet (x-scan 1, x-scan 2) bevor die Translation der Wärmequelle in die y-Koordinatenrichtung wechselt (y-scan 1, y-scan 2). Aufgrund des kontinuierlichen Wärmeeintrags in das Pulverbett sind in der Realität bei konstant bleibenden Parametern eindeutig abgegrenzte Belichtungsfelder zu erwarten.

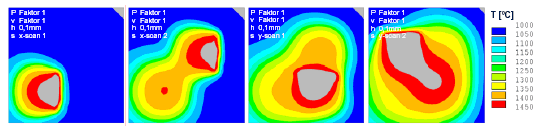
Abbildung 4: Temperaturfeldsimulation mit Ausgangsparamtern
(hatch-Abstand 0,1 mm)

Unter der Prämisse identischer Flächenenergie während der Belichtung wird in der thermischen Strukturberechnung sowohl die Strahlleistung als auch die Scangeschwindigkeit verdoppelt. Der hatch-Abstand von 0,1 mm sowie weitere Prozessrandbedingungen (Strahlung, Konvektion) werden gegenüber den Vorversuchen konstant gehalten. Aus Abbildung 5 geht hervor, dass die Skalierung der Strahlleistung um den Faktor 2 bei doppelter Scangeschwindigkeit nicht ausreichend ist, um ein homogenes Schmelzbad zu gewährleisten. Mit Hilfe dieser Parameterkonfiguration besteht innerhalb der zu Beginn erfolgten Belichtung der x-hatches nur die Möglichkeit, singuläre Spuren zu verfestigen. Demgegenüber ist zu erwarten, dass infolge des sukzessiven Vorwärmens während der Belichtung in x-Richtung die prozesssichere Verfestigung der Flächen mit y-Orientierung der Scanvektoren erfolgen kann.

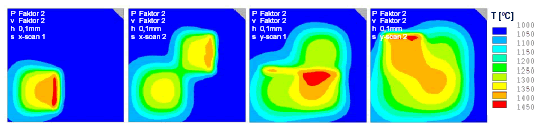
Abbildung 5: Temperaturfeldsimulation mit doppelter Strahlleistung und Scangeschwindigkeit
(hatch-Abstand 0,1 mm)

Weitere Untersuchungen im Rahmen der thermischen Simulation fokussierten sich auf die Variation des hatch-Abstands zwischen 0,1 mm und 0,2 mm. Um auch bei modifizierter Belichtungsstrategie eine identische Flächenenergie zu realisieren, ist es erforderlich, die eingebrachte Leistung der Strahlquelle P um Faktor 2 zu skalieren. Die Ergebnisse der Berechnung zeigen jedoch, dass bei der gewählten Parametervorgabe sehr hohe Spitzentemperaturen resultieren, welche die Prozessstabilität reduzieren. Durch den zu hohen Energieeintrag ist die gegenseitige Abgrenzung einzelner Felder nicht mehr ausreichend gegeben. Bei realen Versuchen sind demzufolge Schmelzbäder ohne definierte Außenkonturen zu erwarten, die erst nach abgeschlossener Belichtung der vollständigen Summe von Teilflächen in den verfestigten Zustand übergehen (vgl. Abbildung 6).

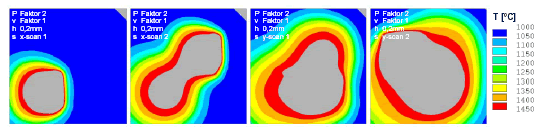
Abbildung 6: Temperaturfeldsimulation mit doppelter Strahlleistung
(hatch-Abstand 0,2 mm)

Die wesentlichen Vorteile der Elektronenstrahltechnologie liegen in der schnellen Strahlablenkung und in der hohen Leistungsdichte. Um dieses Potenzial unter der Prämisse identischer Flächenenergie möglichst effizient zu nutzen, werden in der thermischen Simulation die Strahlleistung gegenüber dem Ausgangsversuch für den hatch-Abstand 0,2 mm um den Faktor 4 erhöht und gleichzeitig die Scangeschwindigkeit verdoppelt (Temperaturfeld siehe Abbildung 7). Eine wesentliche Zielsetzung dieses Versuchs besteht darin, die aus Abbildung 5 und Abbildung 6 ersichtlichen Effekte zu hoher bzw. zu niedriger Prozesstemperaturen zu kompensieren. Die Ergebnisse belegen, dass für den hatch-Abstand von 0,2 mm diese Parameterkonfiguration ähnliche Ergebnisse liefert wie der Ausgangsversuch mit normierten Werten, d. h. einzelne Felder prozesssicher aufgeschmolzen werden können. Das Potenzial der Elektronenstrahltechnologie könnte folglich optimal genutzt werden. Aufgrund der höheren Temperaturgradienten während des Aufheizvorgangs sind gegenüber dem ersten Versuch erhöhte Eigenspannungen bzw. Verzüge zu erwarten. Mit Hilfe einer zeitlich kontrollierbaren Temperaturregelung während der Abkühlphase lassen sich diese Effekte jedoch deutlich minimieren.

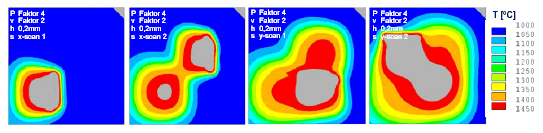
Abbildung 7: Temperaturfeldsimulation mit vierfacher Strahlleitung und doppelter
Scangeschwindigkeit (hatch-Abstand 0,2 mm)

Um die Ergebnisse der numerischen Simulation zu validieren und deren Übertragbarkeit auf den realen Prozess zu untersuchen, werden entsprechende Experimente mit Hilfe einer Elektronenstrahl-Universalkammeranlage durchgeführt ⁸ .

Die Flexibilität der Belichtung einer Pulverschicht durch verschiedene Scanmuster und Strahlparameter wird durch eine geeignete Software gewährleistet, welche in der Lage ist, die Scanmuster der Simulation zu beschreiben (vgl. Abbildung 2). Als Freiheitsgrade, die im realen Versuch direkten Einfluss auf die Energieeinkopplung besitzen, können neben der Vorwärmtemperatur des Pulvers auch Scanstrategie, Scangeschwindigkeit und Strahlleistung sowie Fokusslage identifiziert werden. Als Vorwärmtemperatur wird exakt die Pulvertemperatur bezeichnet, die zum Zeitpunkt der fokussierten Belichtung vorliegt und durch Bestrahlung des Pulvers mit einem defokussierten Elektronenstrahl erzeugt wird. Unter Fokusslage ist der senkrechten Abstand des kleinsten Strahldurchmessers von der Strahlquelle zu verstehen. Bei Variation dieses Abstands durch Veränderung des Stroms entsprechender elektromagnetischer Linsen verändert sich folglich auch die Größe der Auftrefffläche im Pulverbett. In umfangreichen Vorversuchen wurde bisher eine optimale Vorheiztemperatur des Pulvers (ca. 800 °C zum Zeitpunkt der Belichtung) zur Minimierung des Verblasens ermittelt und eine Fokusslage definiert, bei welcher ein guter Schichtzusammenhalt gewährleistet ist.

Als Versuchsträger werden Quadrate mit definierter Kantenlänge und der Schichtdicke von 0,2 mm eingesetzt. Die Oberfläche des Quadrats verfügt über eine hohe Aussagekraft bezüglich der Energieeinbringung in eine Schicht, da weder die geometrische Struktur noch die Temperaturgradienten durch eine darunter liegende Schicht beeinflusst werden. Als Scanvektorlänge wird analog zur Simulation für die Versuche der konstante Wert von 2 mm verwendet.

Als Freiheitsgrade werden hatch-Abstand, Scangeschwindigkeit und Strahlleistung variiert. Auch bei den realen Versuchen werden die Korelationsfaktoren aus der numerischen Simulation bei der Parametervariation verwendet, um letztlich die Übertragbarkeit der Ergebnisse zu gewährleisten. Die in Abbildung 8 dargestellten Parametervariationen lassen erkennen, dass bei allen durchgeführten Versuchen eine identische Flächenenergie in die Pulverschicht eingebracht wird.

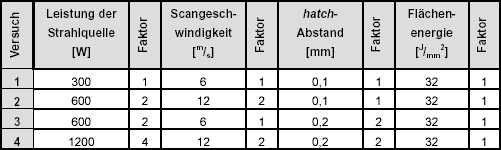
Abbildung 8: Parametervariation der durchgeführten Versuche

In der realen Versuchsumgebung werden die Parameter für den Basisversuch (Versuch 1) so gewählt, dass die einzelnen Belichtungsfelder vollständig aufgeschmolzen werden und sich eine ebene durchgängige Oberfläche ergibt. Wie aus den Simulationsergebnissen gefolgert, ergibt diese Parameterkonfiguration eindeutig abgegrenzte Belichtungsfelder, welche keinen Unterschied zwischen den in x- oder y-Koordinatenrichtung orientierten Feldern erkennen lassen (vgl. Abbildung 9).

Bei gleichzeitiger Verdopplung der Strahlleistung und der Scangeschwindigkeit (vgl. Abbildung 9) ergibt sich ein deutlicher Unterschied zwischen den Belichtungsfeldern in Abhängigkeit der Orientierung der Scanvektoren. So befindet sich in den zuerst belichteten Feldern mit x-hatches nahezu kein verfestigtes Material.

Abbildung 9: Lichtmikroskop-Aufnahmen der durchgeführten Versuchsreihe
(Vergrößerung 15-fach)

Dies weist analog den Simulationsergebnissen daraufhin, dass auf Grund der höheren Scangeschwindigkeit die Energie bei diesen Feldern nicht ausreicht, um das Pulver vollständig aufzuschmelzen. Die eingebrachte Energie führt jedoch zu einer Temperaturerhöhung des gesamten Pulverbetts, wodurch ein Aufschmelzen der entsprechenden Felder bei der nachfolgenden Belichtung der y-hatches resultiert.

In einem weiteren Versuch wird analog zur numerischen Simulation die Strahlleistung verdoppelt und bei konstanter Scangeschwindigkeit der hatch-Abstand von 0,1 mm auf 0,2 mm erhöht. Das Ergebnis des Versuchs (vgl. Abbildung 9) stimmt mit den Aussagen überein, die auf Basis der Simulation getroffen werden können. Vor allem bei den beiden Feldern mit y-hatch ist die Spitzentemperatur zu hoch und das Schmelzbad nimmt deshalb eine undefinierte Kontur an, wodurch eine unregelmäßige Erstarrung bedingt ist. Besonders deutlich wird dies, bei Betrachtung des Übergangs zwischen den beiden Feldern mit y-hatch.

Werden die beiden beschriebenen Variationen unter der Prämisse kombiniert, die Vorteile der Elektronenstrahl-Technologie (hohe Leistungsdichte und hohe Ablenkgeschwindigkeiten) zu nutzen, so ergibt sich die 4-fache Strahlleistung, um bei doppelter Scangeschwindigkeit und hatch-Abstand die gleiche Flächenenergie zu generieren. Die Simulation zeigt an dieser Stelle, dass sich die beiden vorgehenden Effekte in erster Näherung kompensieren und erneut definiert abgegrenzte Schmelzbäder entstehen (vgl. Abbildung 9). In der realen Versuchsumgebung lässt sich diese Tendenz zwar vermuten, jedoch wird diese von einem konkurrierenden Effekt überlagert. Es bilden sich am Rand der einzelnen Felder große Ansammlungen von Schmelze, die nach der Erstarrung einen wulstartigen Rand zurücklassen. Da dieses Ergebnis nicht mit der Simulation erklärbar ist, werden Schmelzbadströmungen und -spannungen verantwortlich gemacht, die erst bei sehr hohen Strahlleistungen und -geschwindigkeiten auftreten aber nicht mit dem bestehenden Modell abgebildet werden können.

Der vorliegende Beitrag zeigt, dass die Vorteile der Verwendung des Elektronenstrahls als Energiequelle bei Metall verarbeitenden generativen Fertigungsverfahren nur dann wirtschaftlich genutzt werden können, wenn ein hohes Prozessverständnis vorhanden ist. Dazu gehört neben der Beherrschung transienter physikalischer Effekte, die in dieser Art und Weise bei anderen Verfahren nicht auftreten, vor allem die Abbildung der Energieeinkopplung mit Hilfe von Methoden der numerischen Struktursimulation.

Die gezeigte mathematische Abstraktion der Strahlquelle in Verbindung mit der Modellierung des Pulverbetts stellt ein effektives Hilfsmittel bei der Parameterauswahl im Vorfeld realer Versuche dar, weil grundsätzliche Tendenzen vorhergesagt werden können. Dies vermindert nicht nur den nötigen experimentellen Aufwand, sondern erhöht auch in besonderem Maße das Prozessverständnis.

Die gezeigte Methodik lässt sich mit geringem Aufwand auf andere generative Verfahren übertragen, auch wenn sich die Art der Strahlquelle (z.B. Laser) oder Werkstoffkennwerte verändern. Nach erneuter Kalibrierung ist das numerische Simulationsmodell auch hier einsetzbar. Damit eröffnet sich die Möglichkeit einer ganzheitlichen Optimierung Metall verarbeitender generativer Verfahren in Bezug auf das thermische und das thermomechanische Verhalten.

[1] Zäh, M. F.; Branner, G.; Hagemann, F.; Lutzmann, S.: Entwicklungstrends im Bereich Rapid Manufacturing. 3D-Erfahrungsforum Werkzeug- und Formenbau, Berlin (2006), S. 263-276.

[2] Zäh, M. F.; Branner, G.; Hagemann, F.: Einführung in generative Fertigungsverfahren und deren Anwendungsfelder. Rapid Manufacturing, Heutige Trends - Zukünftige Anwendungsfelder. Augsburg, München: Herbert Utz 2006, S. 1-21 – 1-39, (iwb Seminarberichte 81).

[3] Zäh, M. F. (Hrsg.); Sigl, M.; Seefried, M.; Hagemann, F.; Kahnert, M.; Müller, A.; Meindl, M.: Wirtschaftliche Fertigung mit Rapid-Technologien. München: Carl Hanser 2006.

[4] Santos, E. C.; Shiomi, M.; Osakada, K.: Rapid Manufacturing of metal components by laser forming. International Journal of Machine Tools & Manufacture 46 (2006) 1459-1468.

[5] Lutzmann, S.; Kahnert, M.; Sigl, M.: Elektronenstrahlsintern als Zukunftstechnologie im Rapid Tooling. Seminarband 81: Rapid Manufacturing. München: Herbert Utz 2006.

[6] Sigl, M.; Lutzmann, S.; Zäh, M. F.: Transient Physical Effects in Electron Beam Sintering. In: Marcus, H.L. et al. (eds.): Solid Freeform Fabrication Symposium Proceedings. Austin, TX. 2006, S. 397-405.

[7] Branner, G.; Lutzmann, S.; Sigl, M.: Optimierung von Scanstrategie und Verzugsverhalten für generative, Metall verarbeitende Fertigungsverfahren. 24th CADFEM Users’ Meeting. International Congress on FEM Technology. October 25 - 27, 2006.

[8] Zäh, M. F.; Kahnert M.: Den Elektronenstrahl für das selektive Sintern von metallischen Werkstoffen nutzen. Proceedings: Euro-u Rapid 2006, International User`s Conference on Rapid Prototyping & Rapid Tooling & Rapid Manufacturing. Frankfurt/Main, November 27th-28th, 2006.

[9] Dobeneck, D.; Löwer, T.; Menhard, C.: Entwicklungspotenziale der thermischen Materialbearbeitung mit Elektronenstrahlen im Vergleich zu Laserstrahlen. Konferenz-Einzelbericht: Strahltechnik, bias Bremen * Band 19 (2002) S. 35-44 (10 Seiten, 17 Bilder). Bremen: BIAS Verlag.

[10] Kruth, J.P.; Froyen, L.; Van Vaerenbergh, J.; Mercelis, P.; Rombouts, M.; Lauwers, B.: Selective Laser Melting on Iron Based Powders. Proceedings of the 14th Int. Symposium on Electromachining. ISEM XIV (2004), Vol.2. Literatur (auch hier wieder eine Überschrift 1) Name, Vorname: Literaturangaben Literaturangaben Literaturangaben:.Gegebenfalls mit

M. F. Zäh
iwb Institut für Werkzeugmaschinen und Betriebswissenschaften
Technische Universität München
Beim Glaspalast 5
86153 Augsburg
Tel: 0821 568830
Fax: 0821 5683350
Email: michael.zaeh@iwb.tum.de
WEB: www.iwb.tum.de

Gerhard Strasser
iwb Institut für Werkzeugmaschinen und Betriebswissenschaften
Technische Universität München
Beim Glaspalast 5
86153 Augsburg
Email: gerhard.strasser@iwb.tum.de
WEB: www.iwb.tum.de

Georg Branner
iwb Institut für Werkzeugmaschinen und Betriebswissenschaften
Technische Universität München
Beim Glaspalast 5
86153 Augsburg
Email: georg.banner@iwb.tum.de
WEB: www.iwb.tum.de

Stefan Lutzmann
iwb Institut für Werkzeugmaschinen und Betriebswissenschaften
Technische Universität München
Beim Glaspalast 5
86153 Augsburg
Email: stefan.lutzmann@iwb.tum.de
WEB: www.iwb.tum.de